| Definitions | f(a), <a, b>, 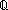 , Id, Type, Top, f(x)?z, x:A , Id, Type, Top, f(x)?z, x:A  B(x), s = t, B(x), s = t,  x:A. B(x), P & Q, Knd, x:A x:A. B(x), P & Q, Knd, x:A  B(x), t.1, t.2, Void, f(x), B(x), t.1, t.2, Void, f(x),  b, b,  A, A,   b, b,  , ,  , ,  x.A(x), x.A(x),   x. t(x), IdDeq, KindDeq, a:A fp x. t(x), IdDeq, KindDeq, a:A fp B(a), product-deq(A;B;a;b), x B(a), product-deq(A;B;a;b), x  dom(f), P dom(f), P   Q, P Q, P    Q, Unit, left + right, M.ef(k,x,s,v)?w, State(ds), timedState(ds), Q, Unit, left + right, M.ef(k,x,s,v)?w, State(ds), timedState(ds),  x x dom(f). v=f(x) dom(f). v=f(x)   P(x;v), M.da(a), z != f(x) P(x;v), M.da(a), z != f(x)   P(a;z), M.rframe(A.sends tfL of k on l), M.sframe(k sends <l,tg>), M.rframe(A.effect f of k on y), M.aframe(k affects x), M.frame(k affects x), M.rframe(A.pre p for a), ma-frame-compat(A;B), M.ds(x), ma-x-tequiv(M;x;s1;s2), Valtype(da;k), M.(timed)state, M.rframe(k reads x), MsgA, read-state(s), (s1 P(a;z), M.rframe(A.sends tfL of k on l), M.sframe(k sends <l,tg>), M.rframe(A.effect f of k on y), M.aframe(k affects x), M.frame(k affects x), M.rframe(A.pre p for a), ma-frame-compat(A;B), M.ds(x), ma-x-tequiv(M;x;s1;s2), Valtype(da;k), M.(timed)state, M.rframe(k reads x), MsgA, read-state(s), (s1  s2 mod x), M.state, t s2 mod x), M.state, t  T, T, 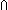 x:A.B(x), Atom$n, inl x , case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , type List, False, P x:A.B(x), Atom$n, inl x , case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , type List, False, P  Q, S Q, S  T, Dec(P), IdLnk, suptype(S; T), s ~ t, {T}, SQType(T) T, Dec(P), IdLnk, suptype(S; T), s ~ t, {T}, SQType(T) |